Next: Computation of the new Up: index Previous: Knot removal - knot
Energy fairing
In principle, the energy fairing works similarly to the knot removal - knot reinsertion method. The main difference
is the relation to fairness criterion (C1) meaning the
local minimization of an energy integral.
Before going into details, we introduce at first some useful notations
which allow a distinction of the different stages of the curve:
- The given curve which is to be faired:
- The B-spline curve which has already been faired by
a certain number of iterations:
- The new curve in the next iteration step:
Then we consider the following local minimization problem: find
a new location
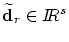 of of
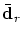 in order
to minimize the energy integral depending on in order
to minimize the energy integral depending on
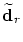
where 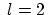 or or 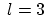 are appropriate choices, as already mentioned in
the introduction. are appropriate choices, as already mentioned in
the introduction.
In addition, the deviation from the original curve 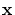 has to be
controlled by a prescribed tolerance has to be
controlled by a prescribed tolerance 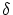 , so we always have to
satisfy the constraint , so we always have to
satisfy the constraint
Now, before we can state the actual fairing algorithm it is necessary to
investigate the following aspects in more detail:
- a)
- how to compute the minimal solution
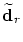 , ,
- b)
- how to fulfil the distance tolerance
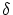 , ,
- c)
- how to rank all control points
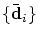 of of
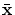 in order to find the location with the best fairing effect
in the next step. in order to find the location with the best fairing effect
in the next step.
Finally, it should be remarked that the integrals (12) obviously
enforce some kind
of continuity in order to be well defined. Doing so, the most convenient way
is to allow at least 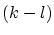 -fold knots in the underlying knot sequence of
the spline curves since the curve is then at least -fold knots in the underlying knot sequence of
the spline curves since the curve is then at least 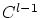 continuous
everywhere. If the knot sequence, however, contains knots with higher
multiplicity then the curve should be split at these knots by treating
the resulting pieces separately. continuous
everywhere. If the knot sequence, however, contains knots with higher
multiplicity then the curve should be split at these knots by treating
the resulting pieces separately.
Subsections
|
![\begin{displaymath}
{\mbox{\bf x}}(t) = \sum_{i=0}^n {\mbox{\bf d}}_i \cdot N_{i,k}(t)
\;\;\; , \;\;\;
t \in [t_{k-1}, t_{n+1}]\;\;\;.
\end{displaymath}](img52.png)
![\begin{displaymath}
\bar{\mbox{\bf x}}(t) = \sum_{i=0}^n \bar{\mbox{\bf d}}_i \cdot N_{i,k}(t)
\;\;\; , \;\;\;
t \in [t_{k-1}, t_{n+1}]\;\;\;.
\end{displaymath}](img53.png)
![\begin{displaymath}
\widetilde{\mbox{\bf x}}(t) = \sum_{\stackrel{\scriptstyle i...
...dot N_{r,k}(t)
\;\;\; , \;\;\;
t \in [t_{k-1}, t_{n+1}]\;\;\;.
\end{displaymath}](img54.png)
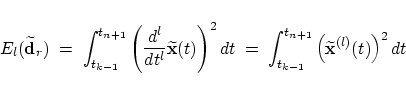
![\begin{displaymath}
\max \{ \vert {\mbox{\bf x}}(t) - \widetilde{\mbox{\bf x}}(t) \vert
\; : \;
t \in [t_{k-1},t_{n+1}] \} \le \delta
\;\;\;.
\end{displaymath}](img62.png)