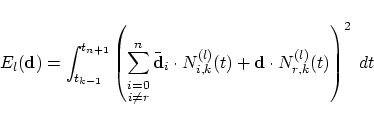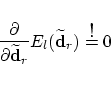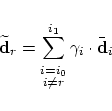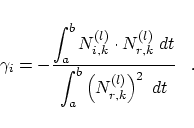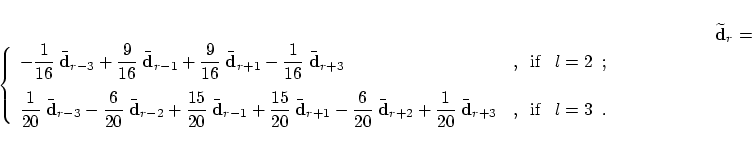DR. JAN HADENFELD
| Next: Distance tolerance Up: Energy fairing Previous: Energy fairing
Writing down the energy integral (12) in more
detail for a general point
|
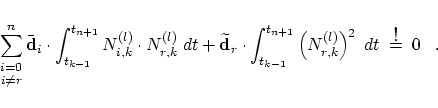 |
(16) |
This single (vector valued) normal equation can
be solved simply. If we additionally take advantage
of
![]() for
for
![]() the solution is
the solution is
Here, some further abbreviations have been already incorporated which are necessary to restrict the integration to the curve interval
| (19) | |||
| (20) |
Moreover, we notice that
![]() is computed
in (17)
by an affine combination of the neighbouring control points
is computed
in (17)
by an affine combination of the neighbouring control points
![]() because we can deduce the following identity
from (18)
because we can deduce the following identity
from (18)
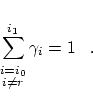 |
(21) |
However, it seems to be a disadvantage that no closed explicit formula
depending only on the actual knot vector ![]() is known for the weights
is known for the weights ![]() in (18). Nevertheless, the weights
in (18). Nevertheless, the weights ![]() can
be computed exactly in a finite number of operations since we are here
dealing with piecewise polynomial basis functions. For example,
we can use a numerical integration method like Gauss quadrature on each interval which works exactly for polynomials of degree
can
be computed exactly in a finite number of operations since we are here
dealing with piecewise polynomial basis functions. For example,
we can use a numerical integration method like Gauss quadrature on each interval which works exactly for polynomials of degree ![]() in order to calculate the appearing integrals in (18).
For more details on integrating products of B-splines we refer to
(Vermeulen et al., 1992).
in order to calculate the appearing integrals in (18).
For more details on integrating products of B-splines we refer to
(Vermeulen et al., 1992).
Again, in the very special case of an equidistant knot vector ![]() and
cubic B-spline curves we can state the formula (17) explicitly:
and
cubic B-spline curves we can state the formula (17) explicitly: