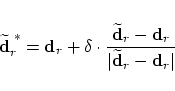 
Next: Ranking number Up: Energy fairing Previous: Computation of the new
Distance tolerance
If we replace the control point
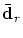 by by
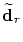 as computed above in (17) then the originally
posed constraint (13), controlling the prescribed as computed above in (17) then the originally
posed constraint (13), controlling the prescribed 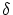 -distance between -distance between 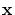 and and
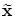 ,
is not yet taken into consideration. ,
is not yet taken into consideration.
In order to overcome this problem we will use the very simple
condition
which guarantees by help of the convex-hull property of B-spline curves that
(13) is fulfilled even if the local fairing step
is repeated several times at different control points.
Condition (23) represents a good upper bound for the actual
pointwise error in (13), at least, if the
polynomial degree of the spline is small; c.f. (de Boor, 1978) and
(Schaback, 1993) where some alternative bounds are discussed.
Now, with respect to (23) we have to distinguish
two cases. The first one is obvious, namely condition
(23) is already fulfilled. Then
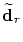 is lying within the is lying within the 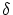 -sphere with the centre -sphere with the centre
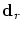 .
In the second case the new control point is situated outside this
sphere and we are therefore interested in that alternative
position .
In the second case the new control point is situated outside this
sphere and we are therefore interested in that alternative
position
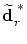 on the boundary of the
distance sphere in which the value of the energy integral on the boundary of the
distance sphere in which the value of the energy integral
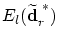 is as small as possible. is as small as possible.
Here, we can use the fact already mentioned that the
isolines of the energy integral are concentric spheres
with centre
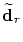 in order to compute the location in order to compute the location
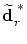 by by
or equivalently as the intersection point of the connecting
line from
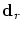 to to
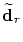 and the and the 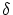 -sphere
around -sphere
around
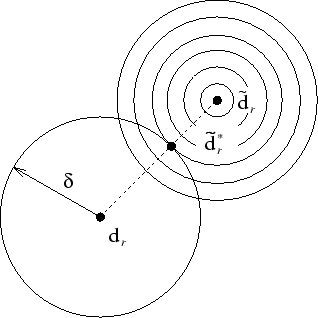
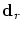 . In Fig. 1 this geometrical situation is
illustrated in the planar case. . In Fig. 1 this geometrical situation is
illustrated in the planar case.
Figure 1: Satisfying the 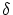 -distance constraint. -distance constraint.
 |
|