Next: The algorithm Up: Energy fairing Previous: Distance tolerance
Ranking number
In the two previous subsections we have learnt how to change
the curve locally by considering a 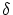 -distance. Now, the
question is: at which point should we fair a given B-spline curve? -distance. Now, the
question is: at which point should we fair a given B-spline curve?
Here, a natural answer is to fair the curve at that control
point
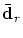 where the largest improvement of the energy
integral is to be expected. where the largest improvement of the energy
integral is to be expected.
Thus, we introduce as a local fairness criterion the following
positive number
or in more detail with help of the notations (10) and
(11)
After some calculations, one verifies directly that (26)
can simply be expressed as
and we recognize that the local criterion (ranking number) is
just the squared improvement of the control point
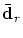 weighted by the integral of the squared and weighted by the integral of the squared and 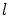 -times differentiated
basis function -times differentiated
basis function 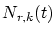 . .
Finally, following the performances of the previous subsection
we can also modify (27) in order to take care of the
distance tolerance 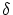 already in the ranking number by using already in the ranking number by using
if
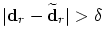 ,
although (28)
is not equivalent to ,
although (28)
is not equivalent to
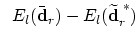 . . |