Next: Examples Up: Energy fairing Previous: Ranking number
The algorithm
We are now ready to summarize the previous developments
to a complete automatic fairing algorithm which, of
course, has the same structure as the algorithm of Farin and Sapidis
already described:
- Compute the ranking numbers
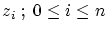 . .
- Find
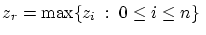 . .
- Compute the new location
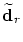 (resp. (resp.
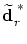 satisfying
the satisfying
the 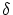 -distance constraint). -distance constraint).
- If a suitable criterion to stop is fulfilled then exit else goto step 1.
There are only two interruptions possible in the present algorithm:
either the number of iterations is restricted or the
algorithm stops if the actual improvement 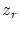 is smaller than a
certain amount. In the examples which we shall present afterwards, we
have always limited the number of iterations. Please note that we
cannot consider the increase of the global fairness criterion is smaller than a
certain amount. In the examples which we shall present afterwards, we
have always limited the number of iterations. Please note that we
cannot consider the increase of the global fairness criterion 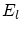 as a possible interruption since its decrease is ensured in
every iteration step. as a possible interruption since its decrease is ensured in
every iteration step.
It is remarkable that the algorithm, as stated above, allows the
modification of all control points. This might not be convenient if we
are dealing with B-splines which itself are part of a composed
spline curve. Thus we always exchange the expression
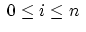 by by
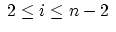 to achieve to achieve 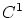 -continuity between the original
and the faired B-spline curve at the two end points.
Similar arguments are valid for continuities of different order. -continuity between the original
and the faired B-spline curve at the two end points.
Similar arguments are valid for continuities of different order.
If the number of control points is large, a faster strategy to get a smooth curve is to determine a so-called ranking list by
ordering all points according to their ranking number. Then this ranking
list can be used as the computational order for the fairing algorithm.
In most cases, it will be sufficient to use only the first quarter of the
ranking list. Afterwards the ranking list should be rebuilt.
This process is repeated 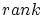 _ _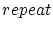 -times whereby -times whereby 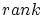 _ _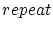 is a variable which will be set individually for every example in the next
subsection. Moreover we realized that it is further advantageous to limit
the number each point can be changed during the algorithm. Doing so, a
only local fairing effect due to the restrictions (23) is avoided. is a variable which will be set individually for every example in the next
subsection. Moreover we realized that it is further advantageous to limit
the number each point can be changed during the algorithm. Doing so, a
only local fairing effect due to the restrictions (23) is avoided.
Finally it should be remarked that the ranking list has to be calculated
only in the first step for all points which can be changed. The reason
is that the control point
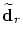 influences
only the ranking numbers influences
only the ranking numbers 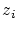 with the index with the index
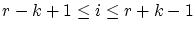 and only these ranking numbers have to be recalculated in the next step. and only these ranking numbers have to be recalculated in the next step. |