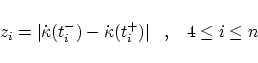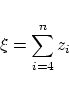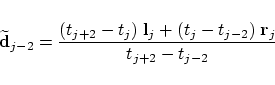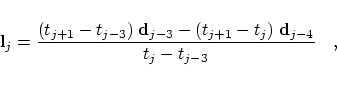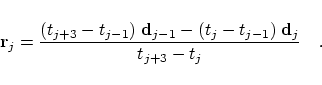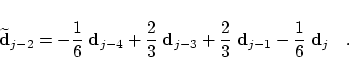 
Next: Energy fairing Up: index Previous: Introduction
Knot removal - knot reinsertion fairing
As already mentioned above the iterative local
fairing method for planar cubic B-spline curves of Farin and
Sapidis is based on fairing criterion (C2). In detail
they observed the following: if the discontinuity
of the slope of the curvature (now differentiated with respect
to the arc length)
at the inner knot 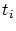 is small then the spline curve is small then the spline curve
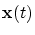 consists of few monotone curvature pieces in the neighbourhood
of the knot consists of few monotone curvature pieces in the neighbourhood
of the knot 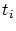 . .
In addition, they concluded that the sum
of all local criteria 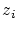 is a reasonable measure to control
the number of monotone curvature pieces of the entire curve. is a reasonable measure to control
the number of monotone curvature pieces of the entire curve.
For the iterative fairing algorithm itself they used the
property of cubic splines that, if the curve is three (instead
of at most two) times differentiable at a point
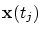 then
the discontinuity then
the discontinuity 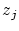 is zero (assuming that the tangent
vector does not vanish at is zero (assuming that the tangent
vector does not vanish at 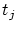 ). Thus, they considered how to
change the curve ). Thus, they considered how to
change the curve
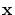 locally so that the continuity order at a
knot locally so that the continuity order at a
knot 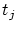 is raised by one. This process, of course, can be
interpreted as a knot removal step with a subsequently performed
knot reinsertion of the knot is raised by one. This process, of course, can be
interpreted as a knot removal step with a subsequently performed
knot reinsertion of the knot 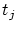 . .
Obviously, the simplest way of doing that is to change only one
control point namely
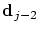 . Then the new location . Then the new location
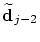 of this control point is given by of this control point is given by
with the two auxiliary points
For example, in the special case of an equidistant knot vector 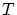 these
formulas simplify to these
formulas simplify to
Here we note that (8) allows a surprising interpretation:
consider the cubic interpolating polynomial
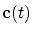 satisfying satisfying
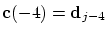 , ,
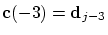 , ,
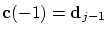 , ,
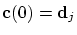 ,
then we simply obtain ,
then we simply obtain
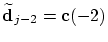 .
On the other hand, a similar interpretation for general knot
vectors could not be found. .
On the other hand, a similar interpretation for general knot
vectors could not be found.
We immediately notice that the (faired) curve with
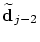 differs from the original curve only
in the interval differs from the original curve only
in the interval
![$]t_{j-2},t_{j+2}[$](img42.png) . Thus this fairing step is local. . Thus this fairing step is local.
Several other possibilities to perform this local changing are discussed
in (Farin et al., 1987) by varying more than one control point in one
local step whereby the changing interval is always increased.
Finally, repeating the above local fairing step subsequently at different
knots (preferably each time at the knot with the largest value of 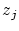 )
Farin and Sapidis have found out in several
numerical tests that the global criterion )
Farin and Sapidis have found out in several
numerical tests that the global criterion 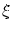 from (4)
always decreases if the iteration number is only large enough. from (4)
always decreases if the iteration number is only large enough.
Altogether, they formulated the following automatic fairing
algorithm:
- Compute
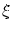 and and
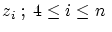 . .
- Find
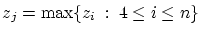 . .
- Compute the new location
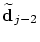 of of
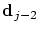 according to (5) - (7). according to (5) - (7).
- If a suitable criterion to stop is fulfilled then exit else goto step 1.
As possible interruptions in (Sapidis and Farin, 1990) it is suggested either
to restrict the number of iterations or to stop if 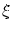 increases resp. if the actual changing of increases resp. if the actual changing of 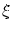 is small enough.
Further, a restriction of the new location is small enough.
Further, a restriction of the new location
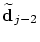 can be built in if a prescribed tolerance of the deviation
should be fulfilled. can be built in if a prescribed tolerance of the deviation
should be fulfilled.
Several examples in (Sapidis and Farin, 1990) illustrate that the fairing
algorithm works well in most cases. Nevertheless, the following peculiarities and questions arise:
- (i)
- the minimization of
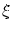 is not ensured in every iteration step, is not ensured in every iteration step,
- (ii)
- the method is restricted to cubic B-spline curves,
- (iii)
- is the local criterion also useful for space curves?
- (iv)
- the new location
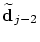 only depends
on the four neighbouring control points only depends
on the four neighbouring control points
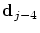 , ,
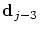 , ,
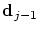 , ,
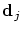 although although
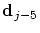 and and
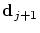 also
influence the interval also
influence the interval
![$]t_{j-2},t_{j+2}[$](img42.png) . .
All these aspects are evaded in the new iterative fairing method
described in the next section. |