DR. JAN HADENFELD
| Next: Knot removal - knot Up: index Previous: Abstract
IntroductionThe usage of piecewise polynomials for the representation of curves and surfaces is very common in modern CAD systems since a lot of requirements like interpolation and approximation are simple and even numerically stable to deal with. However, the designer is not satisfied in every case with the resulting curves or surfaces obtained from such applications since the results might be non-smooth or even unfair meaning that any subjective fairing criterion is offered.Unfortunately, in the literature about fairing a lot of different subjective fairing criteria can be found even for the much simpler case of polynomial spline curves. The two most common definitions for planar curves are the following:
Now in practice these two fairing criteria are not suitable for piecewise polynomials since they lead to non-linear problems whereby explicit solutions cannot be found in general. Therefore, very time-consuming numerical tools are necessary to obtain approximative solutions; see (Moreton, 1993) for criterion (C1) and some similar integral minimization problems. Therefore, in most known fairing algorithms the criterion (C1) is
linearized by the assumption that the actual parameter Nevertheless, it should be kept in mind that the usage of (1)
can produce strange results if the actual parametrization is far
from satisfying
Let us now come back to the problem stated originally. To avoid unfair effects, which can originate from e.g. digitizing errors, two different principles are used in general. The first one consists of incorporating the fairness criterion (1) already into the interpolation or approximation process; see (Hosaka, 1969), (Nowacki, 1990) and (Hagen and Schulze, 1992) for examples and more details. These global methods yield good results although the maximal pointwise error usually cannot be controlled without dealing with non-linear constraints. The second way to obtain smooth spline curves is the separation of the construction and the fairing process. Therefore, the problem of fairing a given spline must be solved. Here, again two principles exist: global one-step algorithms as described in (Kallay, 1993) or local algorithms which have to be executed iteratively; see Section 4 for details. In the case of B-spline curves of order Recently, Farin (1992) developed another local fairing method for cubic B-splines whereby the main part is a degree reduction - degree reelevation step. This method is not considered here although it yields good results, too.
In the present paper we state an alternative local fairing method which is orientated according to criterion (C1) instead of criterion (C2). We locally minimize the linearized energy integral (1) by modifying only one control point in a local step and keeping all others fixed. This idea is also used successfully in a recent paper of Eck and Jaspert (1994) where polygons are faired by minimizing discretized fairness criteria. Furthermore, we also consider the integral over the third instead
of the second derivative as described in (Meier, 1987) and
(Hagen and Schulze, 1990). This criterion, by the way, is equivalent to
the integral over
In Section 3 this iterative fairing method which is valid for B-spline curves of general order with general knot vectors in general dimension is described together with some simple modifications and extensions. It is especially outlined how to satisfy a uniform prescribed bound of the deviation which is important for applications. Further, in Section 4 a general discussion follows where the local and global methods are compared in more detail. In addition, some considerations about local and global convergence of the iterative algorithm can be found. Finally, some concluding remarks and future research directions are contained in Section 5. |
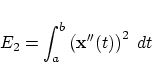
![\begin{displaymath}
{\mbox{\bf x}}(t) = \sum_{i=0}^{n} {\mbox{\bf d}}_i \cdot N_{i,k}(t)
\;\;\;,\;\;\;
t \in [t_{k-1},t_{n+1}]
\end{displaymath}](img14.png)