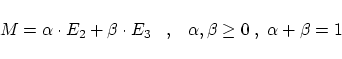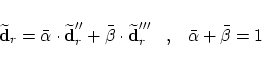DR. JAN HADENFELD
| Next: General discussion Up: Energy fairing Previous: Examples
We have seen in the last part that the two cases of minimization with
respect to |
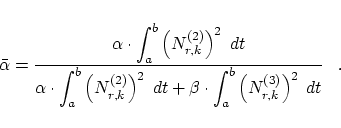 |
(31) |
Now, from (30) we further notice that every point of
the connecting line of
![]() and
and
![]() can be interpreted uniquely as a solution of (29) for certain
fixed values of
can be interpreted uniquely as a solution of (29) for certain
fixed values of ![]() and
and ![]() .
.
This observation can be used to keep the changing of the curve
as small as possible in every iteration step of our fairing algorithms.
Doing so, we define
![]() to be that point
on the connecting line which is as close as possible to
to be that point
on the connecting line which is as close as possible to
![]() whereby
whereby
![]() always has to lie between
always has to lie between
![]() and
and
![]() .
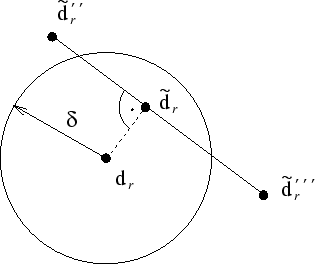
This idea is illustrated in Fig. 9, for the planar case.
.
This idea is illustrated in Fig. 9, for the planar case.
So, obviously a different value of ![]() (resp.
(resp. ![]() ) is chosen
in every step. Therefore, we have found an automatic
determination of these values which are usually preselected.
But because the value
) is chosen
in every step. Therefore, we have found an automatic
determination of these values which are usually preselected.
But because the value ![]() is changed in every iteration step,
the convergence of the algorithm is not ensured. Nevertheless, we
obtained good results with this procedure.
is changed in every iteration step,
the convergence of the algorithm is not ensured. Nevertheless, we
obtained good results with this procedure.
In Fig. 10 the fairing results of the mixed energy method for the curves as given in Fig. 2 and Fig. 5 are demonstrated. We used the same B-spline curves to be able to compare the results.