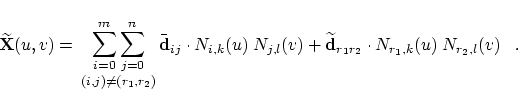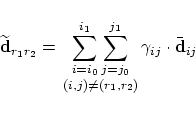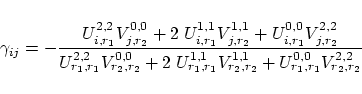Fairing of B-Spline Surfaces

The fairing of B-spline surfaces is very similar to the method for fairing B-spline curves described in section 2. Therefore not all steps are described in detail.

As for curves we want to do the following: a given B-spline surface $\bf X$ has already been faired to a surface $\bar{\bf X}$ . In the following step we want to change only one control point in order to get the smoother surface

$\begin{displaymath} \widetilde{{\bf X}}(u,v) = {\lower 2.2mm \hbox{$\matrix{ {\... ...etilde{\bf d}_{r_1 r_2}\cdot N_{r_1,k}(u)\;N_{r_2,l}(v)\;\;\;. \end{displaymath}$

(41)

This new surface should minimize a given fairness functional like (4), (5) or (6). An existing unique minimum is determined by the control point

$\begin{displaymath} \widetilde{\bf d}_{r_1 r_2} = {\lower 2.1mm \hbox{$\matrix{ ... ...(i,j) \neq (r_1,r_2)} }$}}\gamma_{i j} \cdot\bar{\bf d}_{i j} \end{displaymath}$

(42)

with weighting factors $\gamma_{i j}$ which depend on the fairness functional. In the case of the thin-plate energy (4), the following results are given:

$\begin{displaymath} \gamma_{i j} = - \frac{ U_{i,r_1}^{2,2} V_{j,r_2}^{0,0} + 2\... ...,1} V_{r_2,r_2}^{1,1} + U_{r_1,r_1}^{0,0} V_{r_2,r_2}^{2,2} } \end{displaymath}$

(43)

with the abbreviations for the integrals

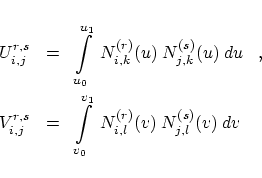$\begin{eqnarray*} U_{i,j}^{r,s} &=& \int \limits_{u_0}^{u_1}\;N_{i,k}^{(r)}(u)\;... ...\int \limits_{v_0}^{v_1}\;N_{i,l}^{(r)}(v)\;N_{j,l}^{(s)}(v)\;dv \end{eqnarray*}$

and for the limits of the integrals and sums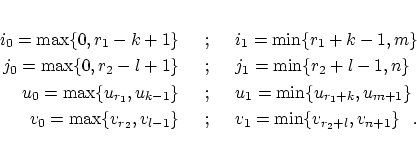

$\begin{eqnarray*} i_0 = \max\{0,r_1-k+1\} \;\;&;&\;\; i_1 = \min\{r_1+k-1,m\}\\ ... ...2},v_{l-1}\} \;\;&;&\;\; v_1 = \min\{v_{r_2+l},v_{n+1}\} \;\,\;. \end{eqnarray*}$

Fairing with a distance tolerance is nearly the same as in the curve case and also the fairing algorithm is the same. So, we do not go into more details in the surface case.

Subsections