DR. JAN HADENFELD
| Next: Fairing of B-Spline Curves Up: Fairing of B-Spline Curves and Surfaces Previous: Fairing of B-Spline Curves and Surfaces
IntroductionIf a designer constructs a B-spline curve or surface with the help of his CAD system or any other application the result might be non-smooth. To avoid this affect, which can originate from e.g. digitizing errors of data points, two different principles are generally used. The first one incorporates a suitable fairness criterion into the interpolation or approximation process; for more informations see [4,17]. The second one is to separate the construction and the fairing process which again can be subdivided into two principles: global methods as described in [20,21,22] and local, iterative methods like [10,12,13,26,27,29]. Our method we are going to describe in the next sections also belongs to the second principle. Although the fairness of a curve or surface can only be described in a
subjective manner the following two definitions are very common in literature
(see also [28]): a (planar) curve is smooth if it minimizes the strain energy of a thin elastic beam described by
where But both fairing criteria lead to a non-linear problem which has to be solved
with the help of numerical tools whereas explicit solutions cannot be given in
general. Following this, both criteria are linearized in most fairing
algorithms. Concerning curves we assume that the parameter In case of given surfaces the functional Another functional suggested in [15] is In this paper a B-spline curve
To smooth a whole curve or surface the following points have to be done:
In the first part of this contribution we want to describe our method for fairing B-spline curves (c.f. [7]) and Bézier-spline curves. A possible solution for fairing rational B-spline curves will also be discussed. The second part contains the extension of this method to surfaces (c.f. [16]). In both parts the benchmark curves and surfaces of the workshop in Lambrecht and some other examples are treated. The results are visualized in some pictures. |
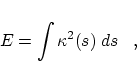
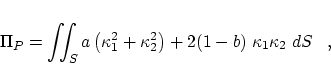
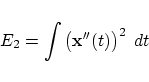
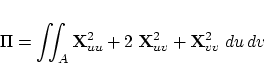
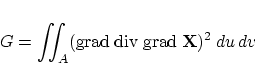
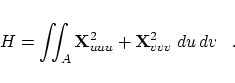
![\begin{displaymath}
{\bf x}(t) = \sum_{i=0}^n {\bf d}_i \cdot N_{i,k}(t)
\;\;\; , \;\;\;t \in [t_{k-1}, t_{n+1}]
\end{displaymath}](img18.png)
![\begin{displaymath}
{\bf X}(u,v) = \sum_{i=0}^m \sum_{j=0}^n\;{\bf d}_{ij} \cdot...
...;\;\;(u,v) \in [u_{k-1},u_{m+1}]\times[v_{l-1},v_{n+1}]\;\;\;,
\end{displaymath}](img23.png)