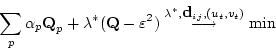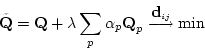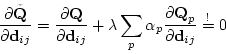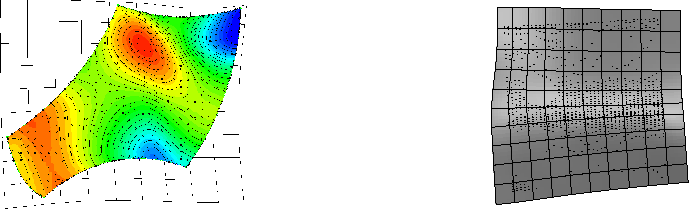DR. JAN HADENFELD
		Glatte Approximation mit B-Spline-Flächen Bei der Erzeugung von parametrisierten Flächen aus Meßpunkten werden üblicherweise in einem ersten Schritt die Punkte parametrisiert; dann wird ein least squares fit durchgeführt. Diese Vorgehensweise hat zwei Nachteile. Es werden nicht die kürzesten Abstände der Punkte zur Fläche minimiert, sondern durch die Parametrisierung induzierte Abstände. Die zwangsläufig nicht optimale Parameterbelegung führt oft auf ein schlecht konditioniertes System beim least squares fit. Die Folge sind unbefriedigende, wellige Flächen. Das vorgestellte Verfahren bestimmt eine optimale Parametrisierung zusammen mit der Fläche in einem iterativen Prozeß. Beim einfachen least squares fit müssen außerdem die Schoenberg-Whitney-Bedingungen erfüllt werden. Dadurch können keine beliebig berandeten Punktmengen oder Punktmengen mit ,,Löchern`` behandelt werden. Durch die Einführung von Energiefunktionalen wird es möglich, auch solche Punktmengen glatt zu approximieren [14,17]. Die Randkurven der Tensorproduktfläche fallen dann nicht mehr mit den Rändern der Punktwolke zusammen. In einem zweiten Schritt wird die berechnete Approximationsfläche an den Rändern der Punktwolke abgeschnitten (siehe Figur (5)). Diese neuen Randkurven werden auch als Trimmkurven bezeichnet und über Splinekurven im Parameterbereich der Fläche beschrieben. Seien nun die fehlerbehafteten Meßpunkte mit $\mbox{P}_i, i=0, \ldots,N-1$ bezeichnet. Zu diesen soll eine energieminimale Tensorprodukt-B-Spline-Fläche $\mbox{X}(u,v)$ berechnet werden, die eine vorgebene Fehlertoleranz $\varepsilon$ einhält. Als Energien werden die Funktionale $\mbox{\bf Q}_i, i=1,\ldots,3$ des Abschnitts 2 verwendet. Der Abstand der gesuchten Fläche zu den Vorgabepunkten wird über $$\mbox{\bf Q}=\frac{1}{N}\sum_i{(\mbox{X}(u_i,v_i)-\mbox{P}_i)^2}$$ (15) erfaßt. Damit läßt sich das Approximationsproblem schreiben als: $$\sum_p {\alpha_p\mbox{\bf Q}_p} \stackrel{\mbox{\bf d}_{ij},... ...box{ unter der Nebenbedingung }\;\; \mbox{\bf Q}<\varepsilon^2$$ (16) Fest vorgegeben sind die Ordnungen $k, l$ und die Knotenvektoren $U,V$ der B-Spline-Fläche sowie die Fehlertoleranz $\varepsilon$ und die skalaren Designparameter $\alpha_p, p=1,\ldots,3$ mit $\sum_p\alpha_p=1$. Die $\alpha_p$ legen den Einfluß der verschiedenen Energien fest und damit die Gestalt der Approximationsfläche. Eine starke Wichtung von $\mbox{\bf Q}_1$ führt zu Flächen mit kleinem Flächeninhalt, von $\mbox{\bf Q}_2$ führt zu Flächen mit geringer Durchbiegung, von $\mbox{\bf Q}_3$ führt zu Flächen mit geringen Krümmungsänderungen. Als Unbekannte hat man die Kontrollpunkte $\mbox{\bf d}_{ij}, i=0,\ldots,n; j=0,\ldots,m$ und die Parameterwerte $(u_i,v_i), i=0,\ldots,N-1$ der Punkte. Der Ansatz mit Lagrange-Multiplikatoren $$\sum_p{\alpha_p\mbox{\bf Q}_p}+\lambda^*(\mbox{\bf Q}-\varep... ...a^*, \mbox{\bf d}_{ij}, (u_t, v_t)}{\longrightarrow}\mbox{min}$$ (17) führt auf ein hochdimensionales, nichtlineares Problem, dessen Lösung mit Standardmethoden zu sehr hohen Rechenzeiten führt. Durch das Festhalten der Kontrollpunkte bzw. der Punktparameterwerte zerfällt das Problem in zwei einfache Teile [5]: für feste Parameterwerte $(u_t,v_t)$ und festes $\lambda^*$ ergibt sich ein lineares Approximationsproblem für feste Kontrollpunkte $\mbox{\bf d}_{ij}$ und festes $\lambda^*$ ergeben sich $N$ 2-dimensionale nichtlineare Unterprobleme, die sogenannten Parameterkorrekturen [8] Damit kann die Flächenapproximation als Iterationsverfahren formuliert werden: Bestimmung einer Startparametrisierung $(u_i,v_i)^0$; $\;\;\;k:=0, \;\; \lambda= \lambda_0\gg 1$ Lösen des linearen Approximationsproblems $\tilde{\mbox{\bf Q}^k}$; $\;\;\;k:=k+1, \;\; \lambda:= \lambda/2$ Berechnung der $(u_i,v_i)^k$ mit Parameterkorrektur Fortfahren mit (2) bis $\mbox{\bf Q}<\varepsilon^2$ Die Startparametrisierung kann durch Projektion der Punkte auf einfache Referenzflächen erfolgen [11]. Die Güte der Parameterwerte spielt hier eine untergeordnete Rolle, da diese Parameterwerte nur eine erste Näherung darstellen. Eine Projektion auf die Ausgleichsebene ist in vielen Fällen ausreichend. Mit $\lambda=1/\lambda^*$ hat das lineare Approximationsproblem die Gestalt $$\tilde{\mbox{\bf Q}}=\mbox{\bf Q}+\lambda\sum_p{\alpha_p\mbo... ... Q}_p} \stackrel{\mbox{\bf d}_{ij}}{\longrightarrow}\mbox{min}$$ (18) Die notwendigen und hinreichenden Bedingungen für ein Minimum $$\frac{\partial\tilde{\mbox{\bf Q}}}{\partial \mbox{\bf d}_{i... ...al \mbox{\bf Q}_p}{\partial \mbox{\bf d}_{ij}}\stackrel{!}{=}0$$ (19) führen auf das lineare Gleichungssystem $$(A+\lambda\sum_p{\alpha_p A_p)}\;d= b \;\;\; \Leftrightarrow \;\;\;\tilde{A}\;d=b$$ (20) Die quadratischen Matrizen 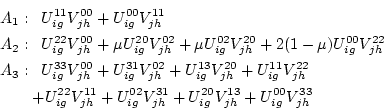$A, A_p$ und $\tilde{A}$ sind alle symmetrisch, positiv semidefinit und besitzen wegen der Lokalität der B-Spline-Funktionen eine dünn besetzte Bandstruktur. $\tilde{A}$ ist darüber hinaus i. allg. regulär und die Lösung damit eindeutig bestimmt. Die Matrix $A$ und die rechte Seite $b$ sind dieselben wie beim least squares fit. Die Einträge der Matrizen $A_p$ ergeben sich zu: $$\begin{eqnarray*} A_1 & : & \;\;U_{ig}^{11}V_{jh}^{00} + U_{ig}^{00}V_{jh}^{11}\... ..._{jh}^{31} + U_{ig}^{20} V_{jh}^{13} + U_{ig}^{00} V_{jh}^{33} \end{eqnarray*}$$ mit den Abkürzungen (9) des Abschnitts 3.3, wobei der Integrationsbereich jedoch nicht eingeschränkt wird. Die Matrizen $A_p$ sind fest über alle Iterationen und müssen deshalb nur einmal zu Beginn berechnet werden. Die Parameterkorrektur in Schritt 3 bestimmt für jeden Punkt die Parameterwerte des Lotfußpunktes auf der Fläche. Die Minimierung wird mit einem 2-dimensionalen Newton-Verfahren durchgeführt. Die Korrekturterme lauten $$%\begin{equation} \left( \begin{array}{c} \Delta u\\ \Delta ... ...\mbox{X}_u\\ (\mbox{X}-\mbox{P})\mbox{X}_v \end{array}\right)$$ und sind unabhängig von den verwendeten Energieintegralen. Das Gesamtverfahren erzeugt anfangs sehr glatte, steife Flächen, die sich in jedem Iterationsschritt besser an die Vorgabepunkte anpassen. Dadurch bleibt die Parameterkorrektur nicht vorzeitig in lokalen Minima hängen; die orthogonale Lage der Fehlervektoren kann im allgemeinen bereits nach ein bis zwei Newton-Schritten erreicht werden. Im Anschluß sind noch einige Beispielflächen teilweise zusammen mit Isophoten dargestellt. In Figur 4 ist ein least squares fit zu sehen und die korrespondierende Fläche, die mit dem vorgestellten Verfahren berechnet wurde. Figur 5 zeigt eine glatte Approximationsfläche zu einer fünfeckig berandeten Punktmenge und eine Approximationsfläche zu einer irregulären Punktmenge mit großen Löchern. Figur 6 schließlich zeigt den least squares fit und die glatte Approximation zu einer komplex strukturierten Punktmenge. Abbildung: least squares fit und glatte Approximationsfläche zu 1448 Punkten Abbildung: Getrimmte Approximationsfläche zu ,,fünfeckiger`` Punktwolke und Approximationsfläche zu ,,löchriger`` Punktmenge Abbildung: least squares fit und glatte Approximationsfläche zu 4101 Punkten