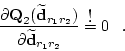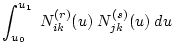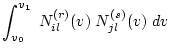DR. JAN HADENFELD
		Der neue Kontrollpunkt Der neue Kontrollpunkt $\widetilde{\mbox{\bf d}}_{r_1 r_2}$ soll so gewählt werden, daß die neue Fläche $\widetilde{\mbox{X}}$ die Biegeenergie minimiert. Diese quadratische Darstellung hat ein eindeutiges Minimum $\widetilde{\mbox{\bf d}}_{r_1 r_2}$, das bestimmt wird durch $$\frac{ \partial \mbox{\bf Q}_2(\widetilde{\mbox{\bf d}}_{r_1... ...bf d}}_{r_1 r_2} } \buildrel \hbox{\large !} \over = 0 \;\;\;.$$ (7) Die Bedingung (7) kann explizit nach dem Kontrollpunkt $\widetilde{\mbox{\bf d}}_{r_1 r_2}$ aufgelöst werden, und wir erhalten $$\widetilde{\mbox{\bf d}}_{r_1 r_2} = {\lower 2.1mm \hbox{$\... 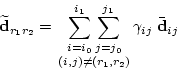...) \neq (r_1,r_2)} }$}} \gamma_{i j}\;\bar{\mbox{\bf d}}_{i j}$$ (8) mit den Faktoren $$\gamma_{i j} = - \frac{ U_{ir_1}^{22} V_{jr_2}^{00} + 2\; U_... ...1r_1}^{11} V_{r_2r_2}^{11} + U_{r_1r_1}^{00} V_{r_2r_2}^{22} }$$ und den Abkürzungen $$U_{ij}^{rs} = \int_{u_0}^{u_1}\;N_{ik}^{(r)}(u)\;N_{jk}^{(s)}(u)\;du$$ (9) $$V_{ij}^{rs} = \int_{v_0}^{v_1}\;N_{il}^{(r)}(v)\;N_{jl}^{(s)}(v)\;dv$$ sowie für die Grenzen der Summen und Integrale $$\begin{eqnarray*} i_0 = \max\{0,r_1-k+1\} \;\;&;&\;\; i_1 = \min\{r_1+k-1,n\}\\ ... 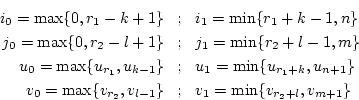...x\{v_{r_2},v_{l-1}\} \;\;&;&\;\; v_1 = \min\{v_{r_2+l},v_{m+1}\} \end{eqnarray*}$$ Es kann gezeigt werden, daß der neue Kontrollpunkt eine affine Kombination der Nachbarkontrollpunkte ist, da $${\lower 2.1mm \hbox{$\matrix{ {\displaystyle \sum_{i=i_0}^{... ...\cr {\scriptstyle (i,j) \neq (r_1,r_2)} }$}}\gamma_{i j} = 1$$ (10) gilt. Diese Eigenschaft (10) kann genutzt werden, um die Berechnung der Integrale zu kontrollieren. Diese können z.B. exakt mit Hilfe der Gauß-Quadratur berechnet werden (s.a. [15]).