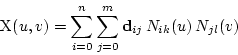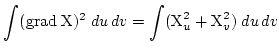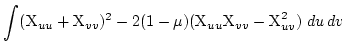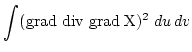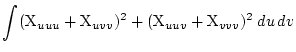next up previous
Next: Iteratives Glätten von B-Spline-Flächen Up: Glätten von Flächen Previous: Problembeschreibung

Flächendarstellungen und Energiemodelle

Werden mit $N_{ik}(t), i=0, \ldots, n$ die B-Spline-Basisfunktionen der Ordnung $k$ (Grad $k-1$) über dem Trägervektor $T=(t_0,...,t_{n+k})$ beschrieben, so lautet eine Parameterdarstellung der Tensorprodukt-B-Spline-Flächen der Ordnung $(k \times l)$ [2,7]


\begin{displaymath} \mbox{X}(u,v) = \sum_{i=0}^{n}\sum_{j=0}^{m} \mbox{\bf d}_{ij}\,N_{ik}(u)\,N_{jl}(v) \end{displaymath} (1)

mit $u \in U, \; v \in V$ und $U,V$ als zugehörige Trägerbereiche. Die $\mbox{\bf d}_{ij}$ werden Kontrollpunkte oder de Boor-Punkte genannt, sie sind affin invariant mit der Fläche verbunden. Das von den $\mbox{\bf d}_{ij}$ durch lineares Verbinden von Nachbarpunkten mit festem $i$ bzw. festem $j$ entstehende (Kontroll-)Netz beschreibt ungefähr den Verlauf der Fläche. Wird ein Kontrollpunkt verändert, so ergibt sich eine lokale Deformation der vorliegenden Fläche.

Als Energiemodelle zur Beschreibung einer glatten Oberfläche sollen quadratische Operatoren benutzt werden, da diese beim Differenzieren (für das Berechnen der Minima) auf lineare und damit schnell arbeitende Algorithmen führen. Im folgenden liegen als Energiemodelle zugrunde [3]


$\displaystyle \mbox{\bf Q}_1$ $\textstyle =$ $\displaystyle \int_{}^{} (\mbox{grad}\;\mbox{X})^2\; du\,dv = \int_{}^{} (\mbox{X}_u^2 + \mbox{X}_v^2)\; du\,dv$ (2)
$\displaystyle \mbox{\bf Q}_2$ $\textstyle =$ $\displaystyle \int_{}^{} (\mbox{X}_{uu} + \mbox{X}_{vv})^2 - 2(1 - \mu)(\mbox{X}_{uu}\mbox{X}_{vv} - \mbox{X}_{uv}^2)\; du\,dv$ (3)
$\displaystyle \mbox{\bf Q}_3$ $\textstyle =$ $\displaystyle \int_{}^{} (\mbox{grad div grad}\;\mbox{X})^2\; du\, dv$  
  $\textstyle =$ $\displaystyle \int_{}^{}(\mbox{X}_{uuu} + \mbox{X}_{uvv})^2 + (\mbox{X}_{uuv} + \mbox{X}_{vvv})^2\; du\,dv$ (4)

Diese Ansätze haben sich bisher (unter verschiedenen anderen Gesichtspunkten) bestens bewährt.