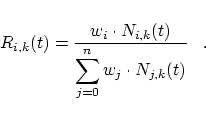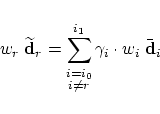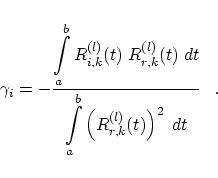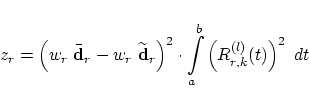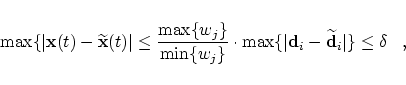DR. JAN HADENFELD
		Fairing of Rational B-Spline Curves Although the use of rational B-splines is not very common in CAD systems most of them can handle NURBS. One reason is that most of the algorithms for integral B-splines like the de Boor or the knot insertion algorithm can simply extend to rational B-splines but it is difficult for the designer to handle control points and weights. A rational B-spline curve is defined by $${\bf x}(t) = \frac{\displaystyle \sum_{i=0}^n w_i \; {\bf d}... ...dot N_{i,k}(t)} \;\;\; , \;\;\;t \in [t_{k-1}, t_{n+1}]\;\;\;,$$ (34) whereas the $w_i$ are the so-called weights. We assume $w_i > 0$. Another spelling for (34) is $${\bf x}(t) = \sum_{i=0}^n {\bf d}_i \cdot R_{i,k}(t) \;\;\; , \;\;\;t \in [t_{k-1}, t_{n+1}]$$ (35) with the rational basis functions $$R_{i,k}(t) = \frac{\displaystyle w_i \cdot N_{i,k}(t)} {\displaystyle \sum_{j=0}^n w_j \cdot N_{j,k}(t)}\;\;\;.$$ (36) More details about NURBS can be found e.g in [9,25]. In [18] a fairing method for NURBS is presented. In an optimization process the authors calculate a new set of weights to get a smoother curve. In contrast to their method we fixed the weights to get a linear problem. Doing the same steps as for integral curves the new control point $\widetilde{\bf d}_r$ is determined by $$w_r \; \widetilde{\bf d}_r = \sum_{\stackrel{\scriptstyle i=... ...criptstyle i \ne r}}^{i_1} \gamma_i \cdot w_i \; \bar{\bf d}_i$$ (37) with the weighting factors $\gamma_i$ of the form $$\gamma_i = - \frac {\displaystyle \int \limits_a^b R_{i,k}^{... ...t \limits_a^b \left( R_{r,k}^{(l)}(t) \right)^2 \; dt} \;\;\;.$$ (38) The new control point is also an affine combination of the involved one but the integrals can not be calculated exactly as in the non-rational case. We use the Romberg quadrature to integrate the products of the rational basis function; see [2]. The ranking-number $$z_r = \left(w_r \; \bar{\bf d}_r - w_r \; \widetilde{\bf d}_... ...\cdot \int \limits_a^b \left( R_{r,k}^{(l)}(t) \right)^2 \; dt$$ (39) looks also very similar to the non-rational case. If we want to fair with a distance tolerance we can use the upper bound $$\max \{ \vert {\bf x}(t) - \widetilde{\bf x}(t) \vert \le \f... ...vert {\bf d}_i - \widetilde{\bf d}_i\vert \} \le \delta\;\;\;,$$ (40) which is a (roughly) upper bound for (19) in the rational case.